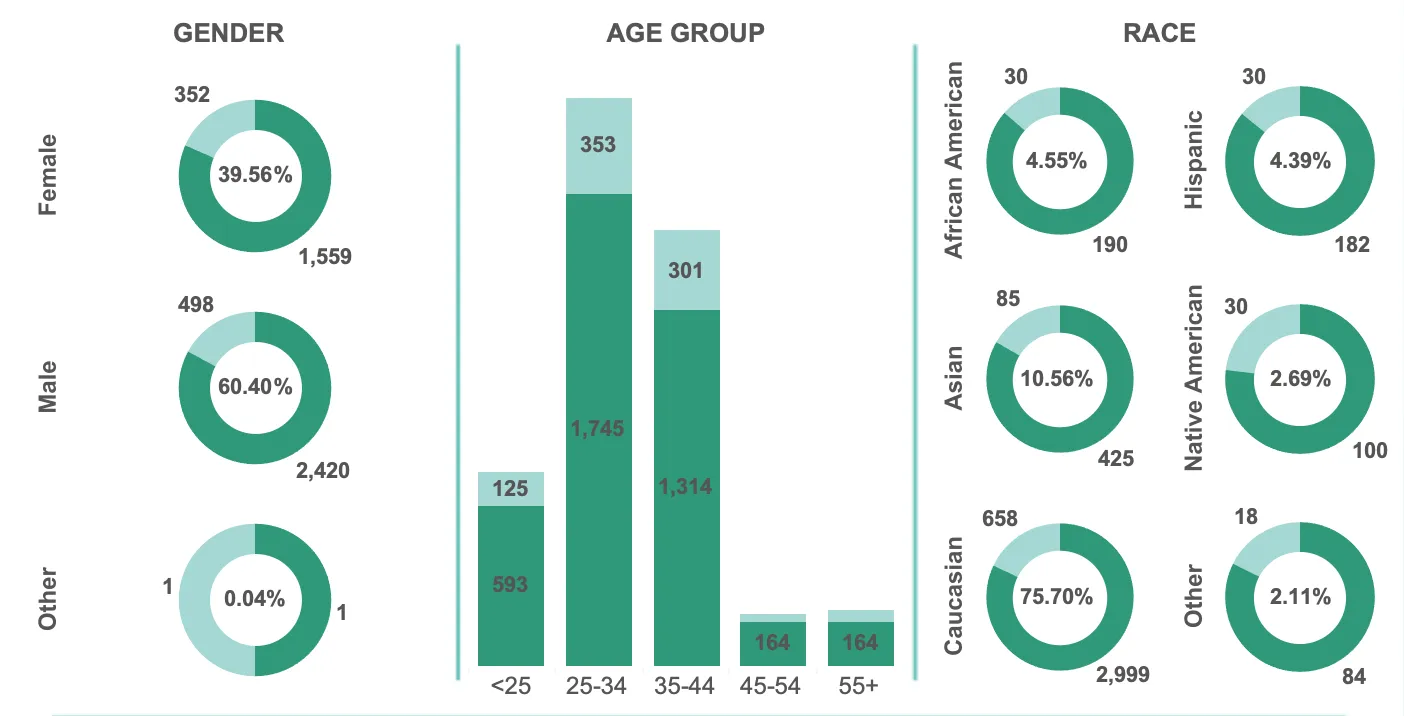
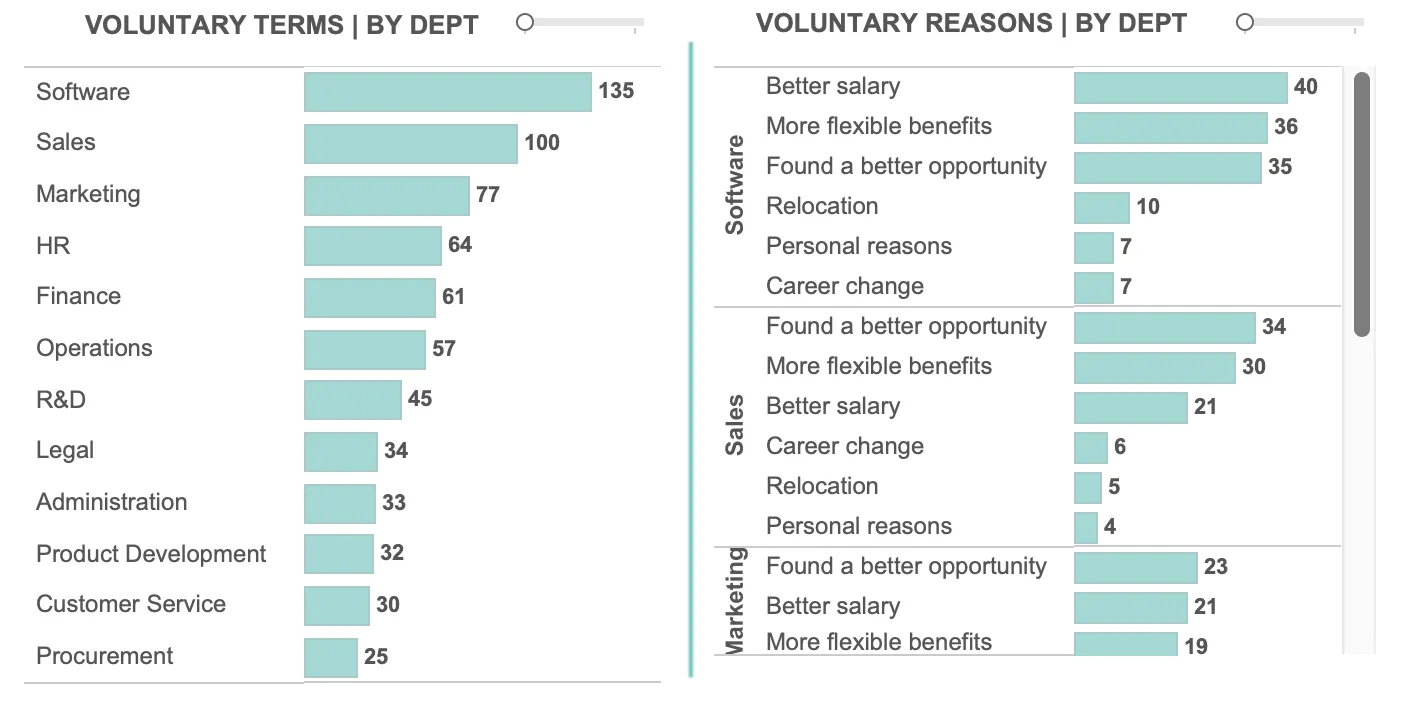
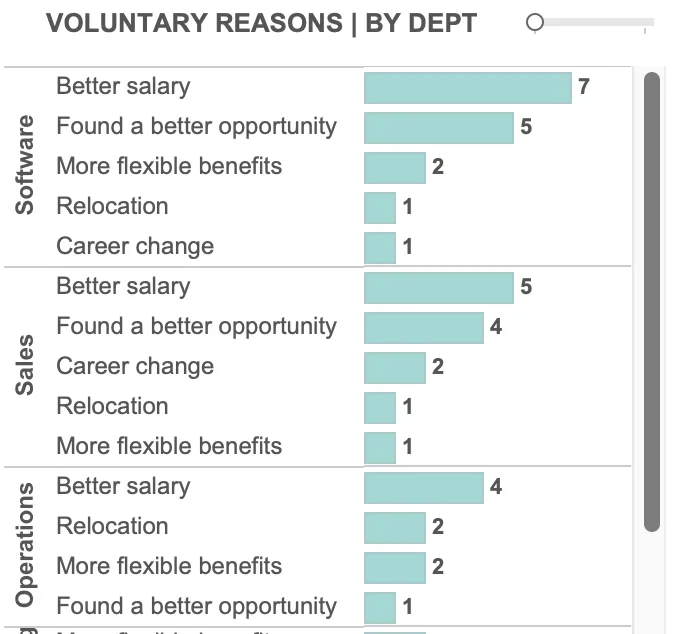
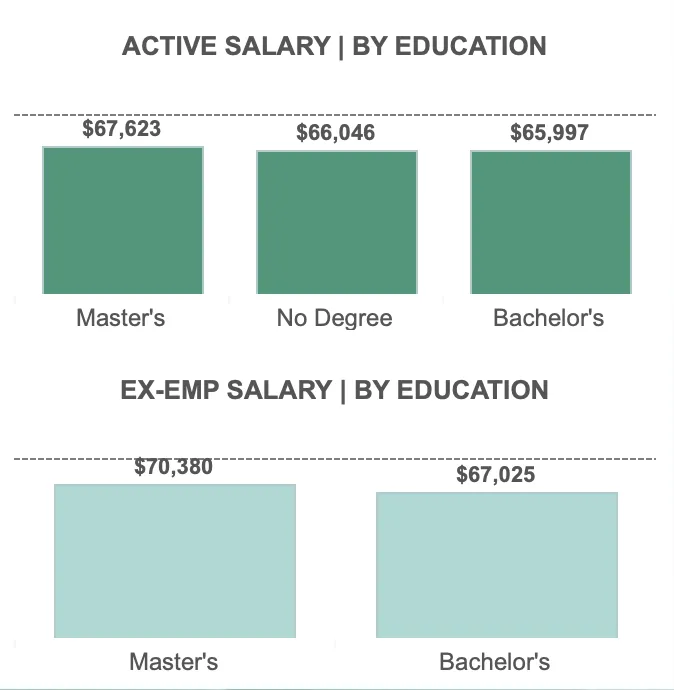
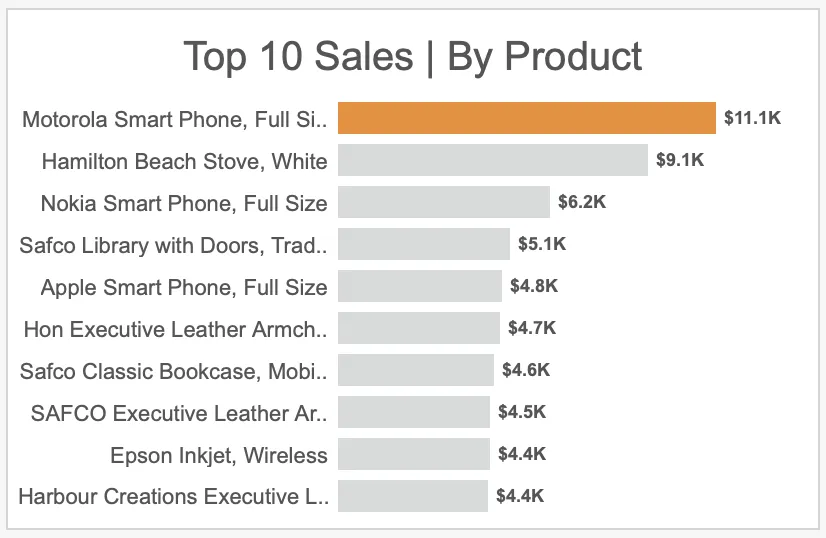
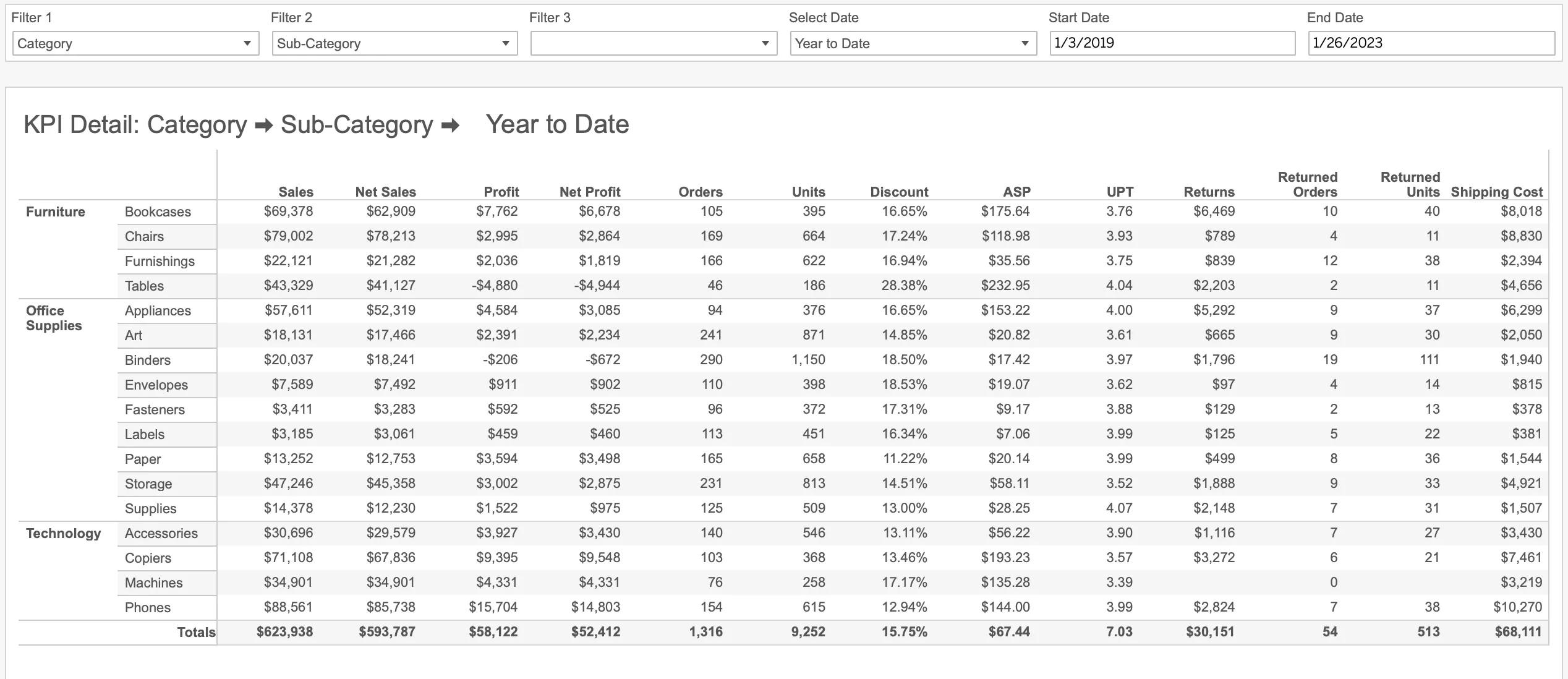
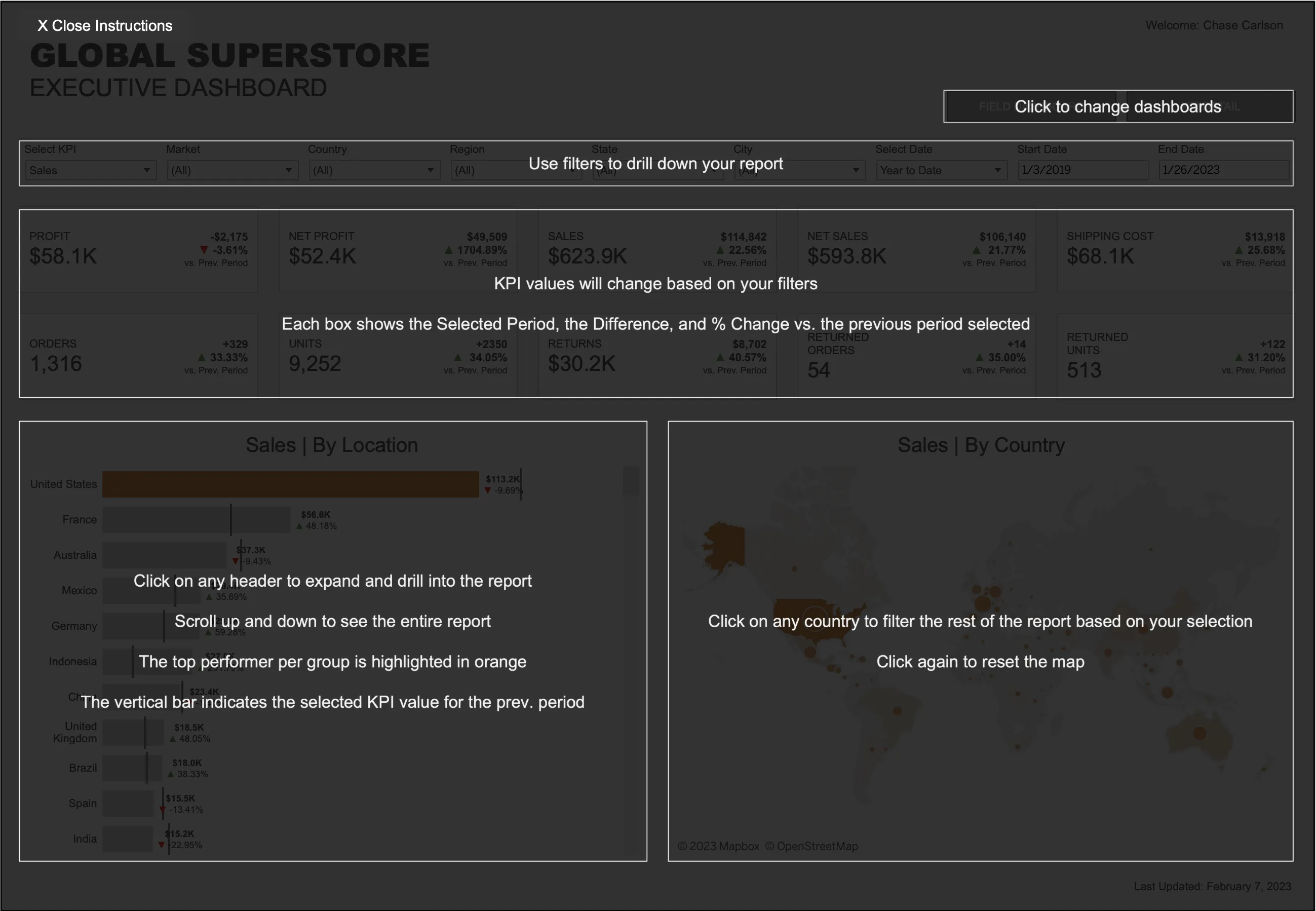
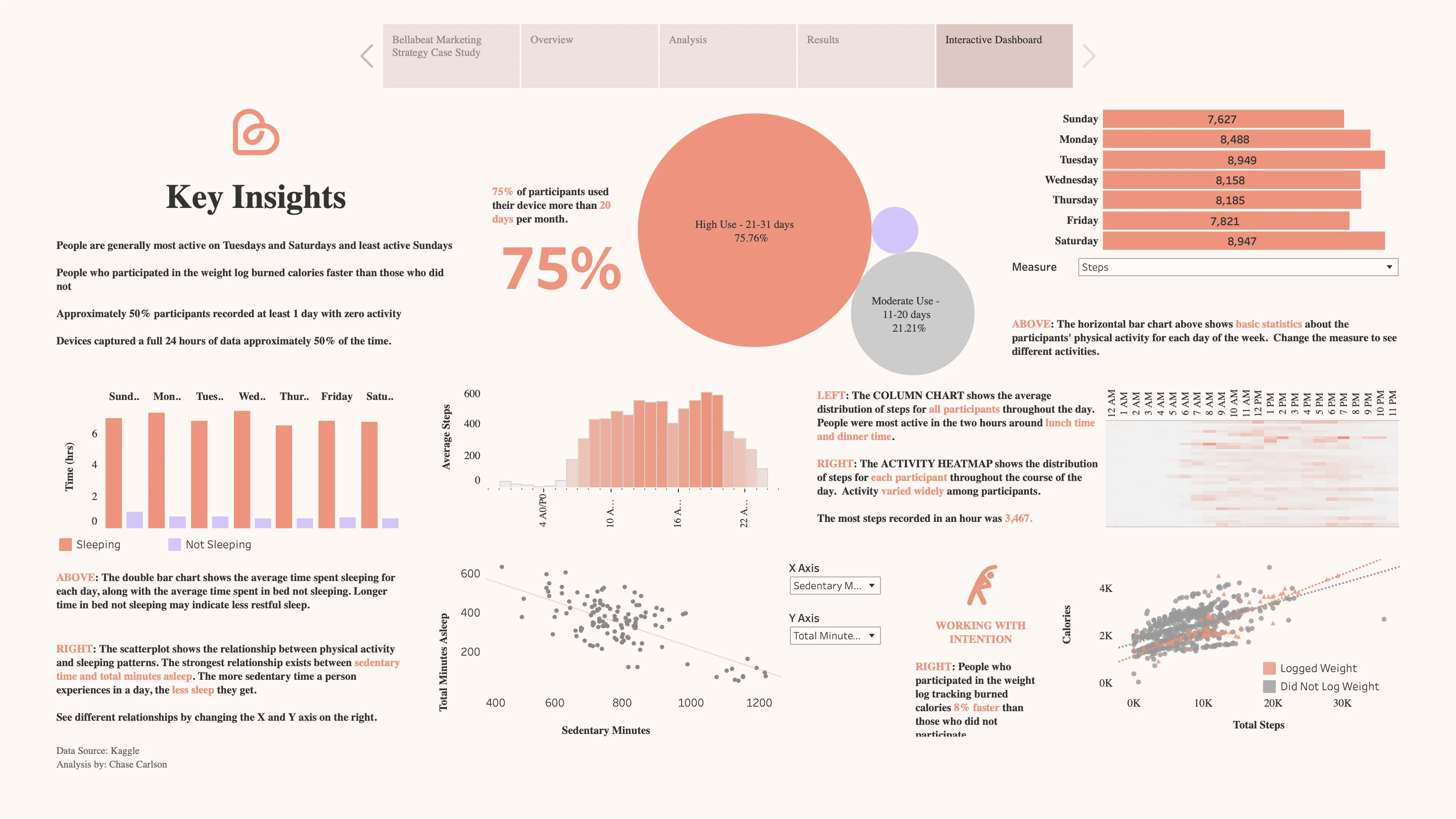
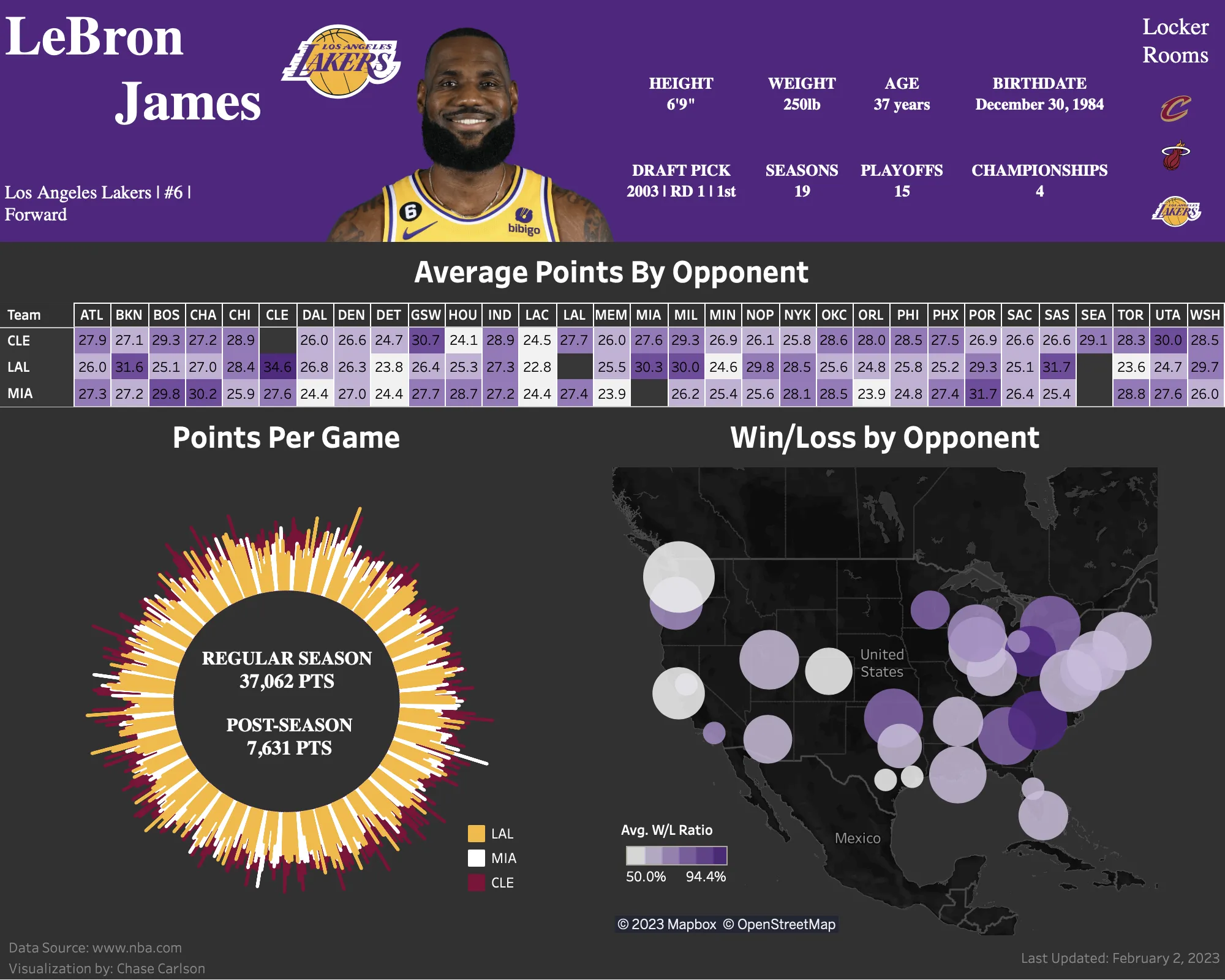
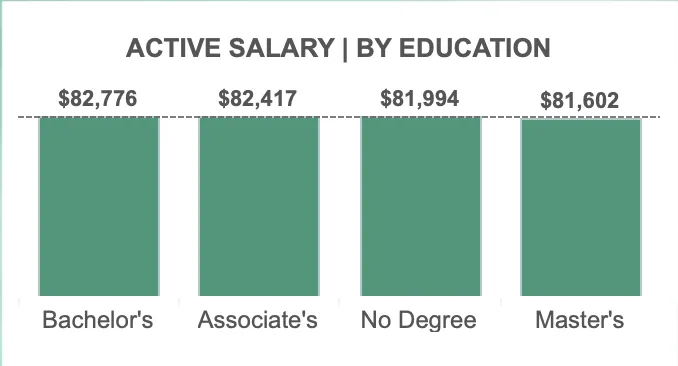Global supply chains are complex systems responsible for moving products from multiple origin
locations to various transshipment points (such as distribution centers), and finally to their
intended destinations. In supply chain management, one of the primary challenges is solving the
transportation problem, which involves determining the optimal number of units to ship across each
segment of the network. The objective is to ensure that all destination demands are met while
minimizing transportation costs.
Supply chain managers must strategically allocate resources to achieve cost-effective and efficient
distribution. However, this task is complicated by the need to balance multiple variables, including
production capacity, demand requirements, and transportation costs. Linear programming provides a
mathematical approach to solving these network flow problems, enabling the most efficient movement
of goods across the distribution network while minimizing costs and satisfying demand requirements.
The Problem
For this example I selected the following case problem from the textbook Introduction to
Management Science: Quantitative Approach:
The Darby Company manufactures and distributes meters used to measure electric power
consumption. The company started with a small production plant in El Paso and gradually
built a customer base throughout Texas. A distribution center was established in Fort Worth,
Texas, and later, as business expanded, a second distribution center was established in
Santa
Fe, New Mexico.
The El Paso plant was expanded when the company began marketing its meters in Arizona,
California, Nevada, and Utah. With the growth of the West Coast business, the Darby Company
opened a third distribution center in Las Vegas and just two years ago opened a second
production plant in San Bernardino, California.
Manufacturing costs differ between the company’s production plants. The cost of each meter
produced at the El Paso plant is $10.50. The San Bernardino plant utilizes newer and more
efficient equipment; as a result, manufacturing cost is $0.50 per meter less than at the El
Paso
plant.
Due to the company’s rapid growth, not much attention had been paid to the efficiency of its
supply chain, but Darby’s management decided that it is time to address this issue. The cost
of shipping a meter from each of the two plants to each of the three distribution centers is
shown in Table 6.10.
The quarterly production capacity is 30,000 meters at the older El Paso plant and 20,000
meters at the San Bernardinoplant. Note that no shipments are allowed from the San
Bernardino plant to the Fort Worthdistribution center.
The company serves nine customer zones from the three distribution centers. The forecast of
the number of meters needed in each customer zone for the next quarter is shownin Table
6.11.
The cost per unit of shipping from each distribution center to each customer zone is given
in Table 6.12; note that some distribution centers
cannot serve certain customer zones.
These are indicated by a dash, “—”.
In its current supply chain, demand at the Dallas, San Antonio, Wichita, and Kansas City
customer zones is satisfied by shipments from the Fort Worthdistribution center. In a
similar
manner, the Denver, Salt Lake City, and Phoenix customer zonesare served by the Santa Fe
distribution center, and the Los Angeles and San Diego customer zones are served by the Las
Vegas distribution center. To determine how many units to ship from each plant, the
quarterly
customer demand forecasts are aggregated at the distribution centers, and a transportation
model
is used to minimize the cost of shipping from the production plants to the distribution
centers.
Table 6.10 SHIPPING COST PER UNIT FROM PRODUCTION PLANTS
TO DISTRIBUTION CENTERS (IN $)
|
Distribution
Center
|
|
Plant |
Fort Worth |
Santa Fe |
Las Vegas |
| El Paso |
3.20 |
2.20 |
4.20 |
| San Bernardino |
— |
3.90 |
1.20 |
Table 6.11 QUARTERLY DEMAND FORECAST
| Customer Zone |
Demand (meters) |
| Dallas |
6300 |
| San Antonio |
4880 |
| Wichita |
2130 |
| Kansas City |
1210 |
| Denver |
6120 |
| Salt Lake City |
4830 |
| Phoenix |
2750 |
| Los Angeles |
8580 |
| San Diego |
4460 |
Table 6.12 SHIPPING COST FROM THE DISTRIBUTION CENTERS
TO CUSTOMER ZONES
|
Customer
Zone
|
|
Distribution Center |
Dallas |
San Antonio |
Wichita |
Kansas City |
Denver |
Salt Lake City |
Phoenix |
Los Angeles |
San Diego |
| Fort Worth |
0.3 |
2.1 |
3.1 |
4.4 |
6.0 |
— |
— |
— |
— |
| Santa Fe |
5.2 |
5.4 |
4.5 |
6.0 |
2.7 |
4.7 |
3.4 |
3.3 |
2.7 |
| Las Vegas |
— |
— |
— |
— |
5.4 |
3.3 |
2.4 |
2.1 |
2.5 |
Managerial Report
You are asked to make recommendations for improving Darby Company's supply chain by answering
the
following questions:
- Draw a network representation of the Darby company's current supply chain map. If the
company does not change its current supply chain, what will its distribution costs be for
the following quarter?
- Suppose that the company is willing to consider dropping the distribution center
limitations; that is, customers could be served by any of the distribution centers for which
costs are available. Can costs be reduced? If so, by how much?
- The company wants to explore the possibility of satisfying some of the customer demand
directly from the production plants. In particular, the shipping cost is $0.30 per unit from
San Bernardino to Los Angeles and $0.70 from San Bernardino to San Diego. The cost for
direct shipments from El Paso to San Antonio is $3.50 per unit. Can distribution costs be
further reduced by considering these direct plant-tocustomer shipments?
Solution 1
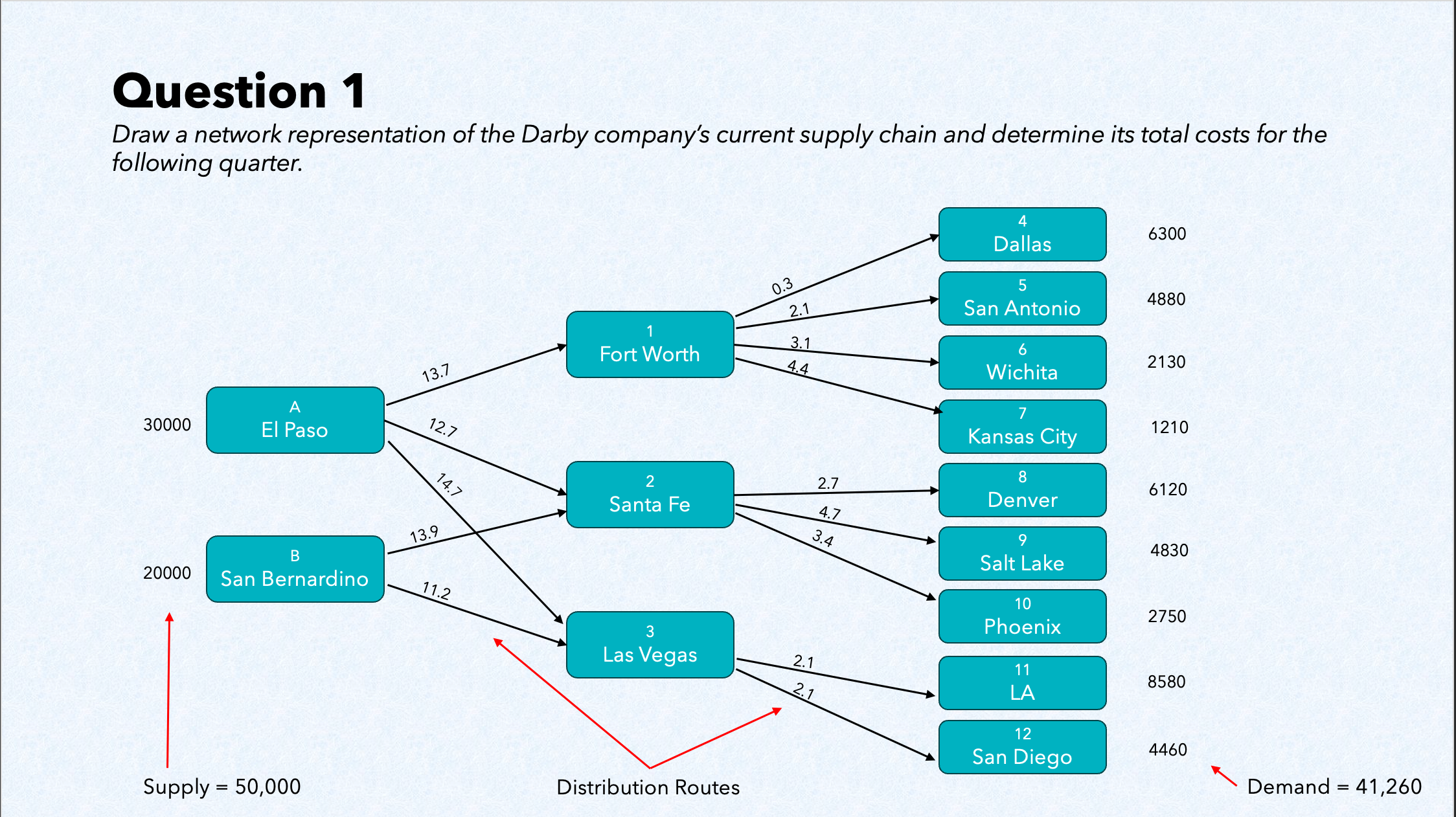
The first step is to draw a supply chain map showing all of the potential shipment arcs out of
the production plants and distribution centers under the current structure. Figure 1 shows
graphically the 14 distribution routes (arcs) Darby company can use. The ammount of supply
available is written next to each origin node, and the amount of demand is written next to each
destination node. The cost per unit of shipping from each node is written on the arc for each
route.
A linear programming model is used to solve this transshipment problem to determine the minimum
cost under the given constraints. I used double-subscripted decision variables based on the
labels I gave in the network diagram above, with XA1 denoting the number of units
shipped from origin A (El Paso) to destination 1 (Fort Worth), XA2 denoting the number of units
shipped from origin A (El Paso) to destination 2 (Santa Fe), and so on.
Because the objective is to minimize the total transportation cost, I used the cost data in
Table 6.12 or on the arcs in Figure 1 to develop the following objective function:
Min 13.7XA1 +
12.7XA2 +
14.7XA3 +
13.9XB2 +
11.2XB3 +
0.3X14 +
2.1X15 +
3.1X16 +
4.4X17 +
2.7X28 +
4.7X29 +
3.4X210 +
2.1X311 +
2.5X312
This objective function ensures the lowest total cost through all possible distribution routes.
Transshipment problems also require several constraints for each of the shipment nodes. For
origin nodes, the sum of the shipments out minus the sum of the shipments in must be
less than or equal to the origin supply. For destination nodes, the sum of the shipments in
minus the sum of shipments out must equal demand. For transshipment nodes, the sum of the
shipments out must equal the sum of the shipments in.
Based on the requirements listed in the problem description, I came up with the following
constraints:
El Paso supply constraint:
XA1 +
XA2 +
XA3 ≤ 30000
San Bernardino supply constraint:
XB2 ≤ 20000
Fort Worth transshipment node:
(X14 +
X15 +
X16 +
X17) -
XA1 = 0
Santa Fe transshipment node:
(X28 +
X29 +
X210) -
(XA2 +
XB2) = 0
Las Vegas transshipment node:
(X311 +
X312) -
(XA3 +
XB3) = 0
Dallas demand constraint:
X14 ≥ 6300
San Antonio demand constraint:
X15 ≥ 4880
Wichita demand constraint:
X16 ≥ 2130
Kansas City demand constraint:
X17 ≥ 1210
Denver demand constraint:
X28 ≥ 6120
Salt Lake City demand constraint:
X29 ≥ 4830
Phoenix demand constraint:
X210 ≥ 2750
Los Angeles demand constraint:
X311 ≥ 8580
San Diego demand constraint:
X312 ≥ 4460
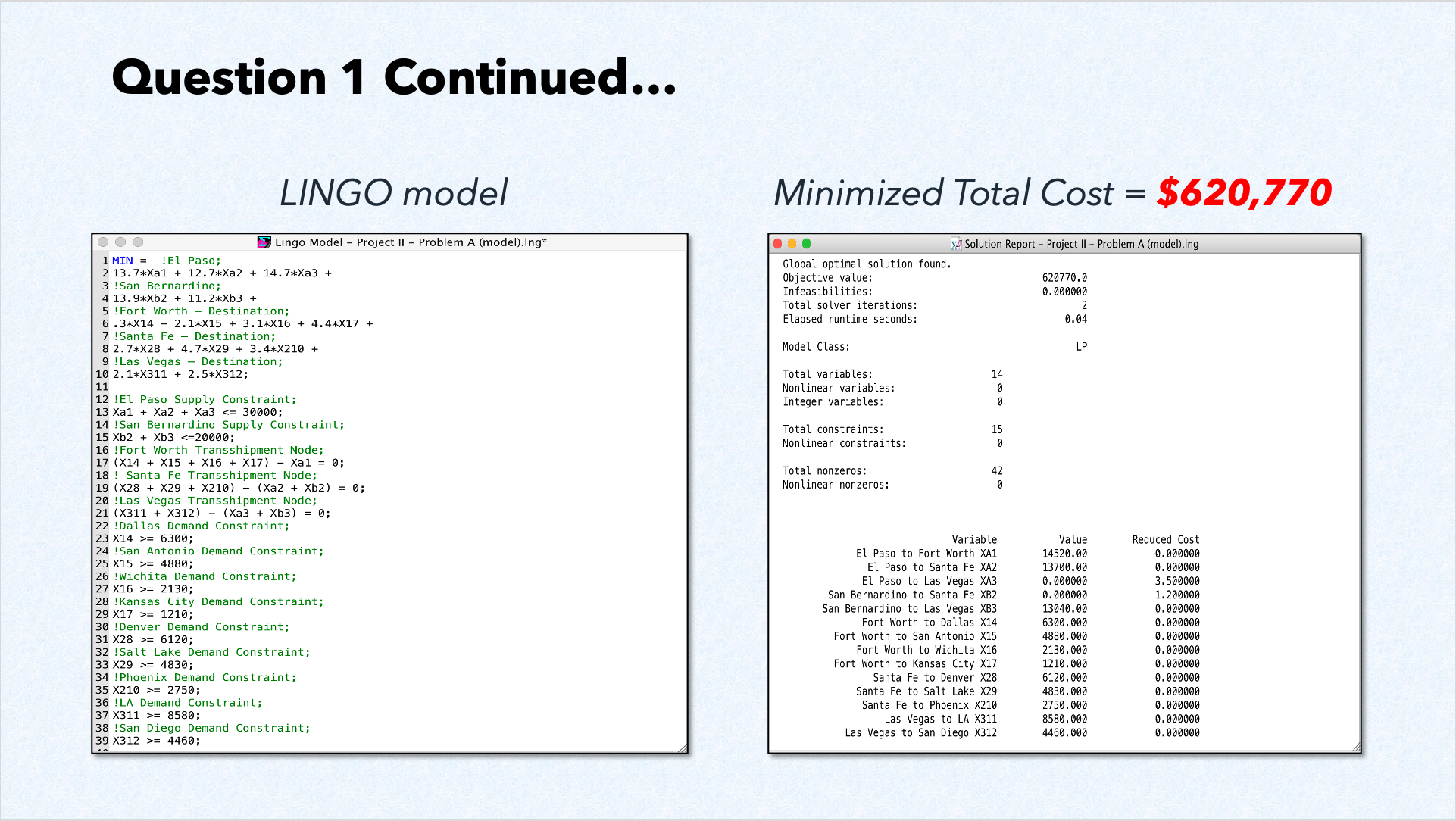
The LINGO model and solution report are included in Figure
2 below:
Figure 2. Optimal solution with current constraints
The optimal solution projects that total transportation costs for the next quarter, given the
current constraints, will amount to $620,770. The El Paso plant is slated to ship 14,520 units
to the Fort Worth Distribution Center and 13,700 units to the Santa Fe Distribution Center. The
San Bernardino plant, however, is expected to ship only 13,840 of its 20,000-unit capacity to
Las Vegas, with no shipments to Santa Fe. At the Fort Worth Distribution Center, 6,300 units
will be distributed to Dallas, 4,880 units to San Antonio, 2,130 units to Wichita, and 1,210
units to Kansas City. Meanwhile, the Santa Fe Distribution Center will dispatch 6,120 units to
Denver, 4,830 units to Salt Lake City, and 2,750 units to Phoenix. Lastly, the Las Vegas
Distribution Center will distribute 8,580 units to Los Angeles and 4,460 units to San Diego.
Solution 2
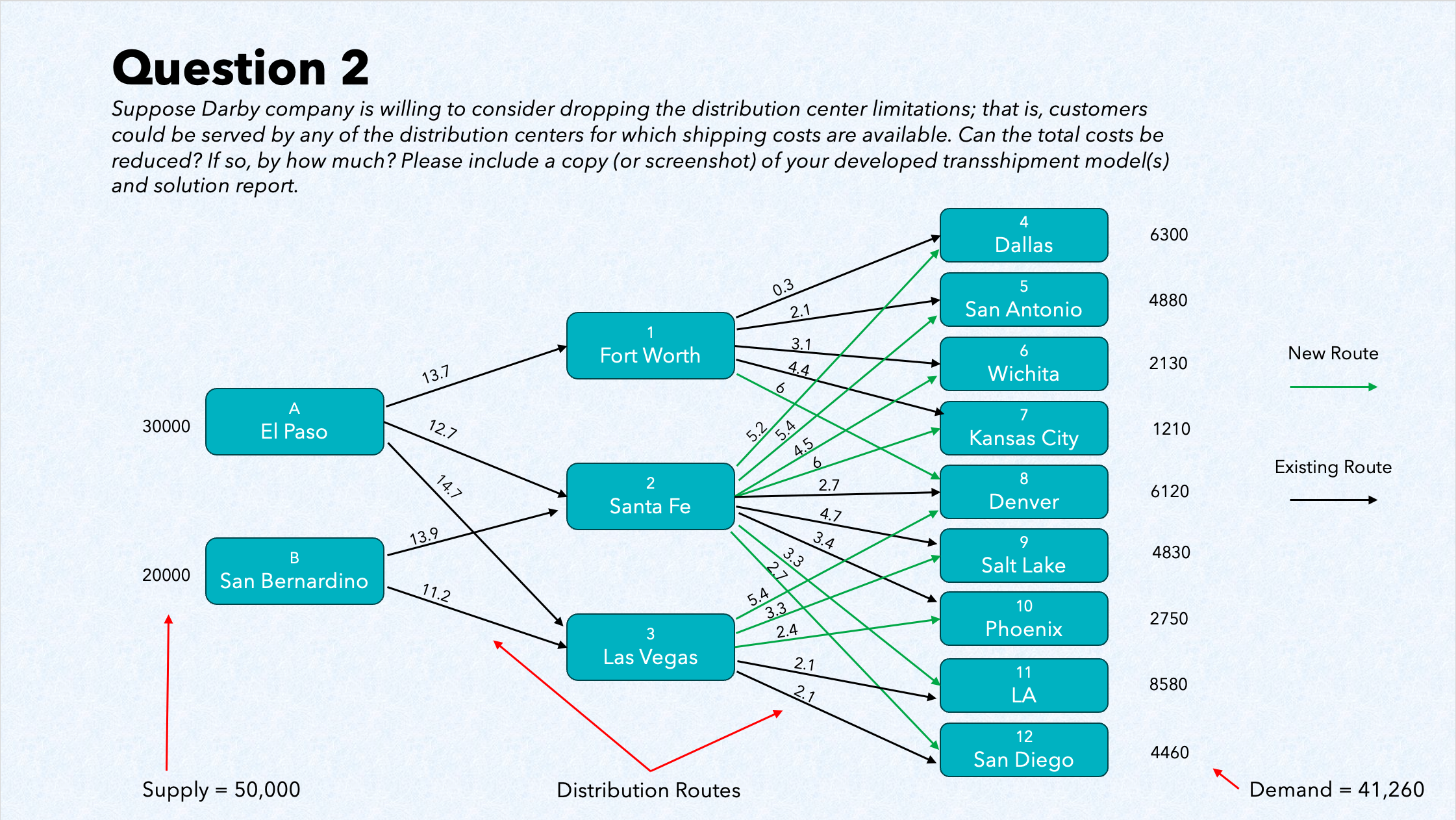
To determine if costs can be reduced if the company is willing to consider dropping the
distribution center limitations, I present an updated graphic representation of the distribution
network along with a modified linear program below in Figure
3 and Figure 4.
Figure 3. Modified distribution network diagram
The green arrows highlight new potential distribution routes. Fort Worth can now ship to
customers in Denver, while Santa Fe can extend its reach to customers in Dallas, San Antonio,
Wichita, Kansas City, Los Angeles, and San Diego. Additionally, Las Vegas can now serve
customers in Denver, Salt Lake City, and Phoenix. The supply and demand levels remain unchanged,
as do the restrictions on the origin nodes.
Figure 4. Optimal solution without distribution
center limitations
If Darby Company were to lift the distribution center restrictions, it could save a total of
$19,828 in shipping costs. By adjusting the constraints, some of the demand could be shifted
from the El Paso production plant to the San Bernardino plant, allowing it to ship its full
capacity (20,000 units) to Las Vegas. Since the transportation costs per unit are lower from Las
Vegas to Salt Lake City ($3.30) and from Las Vegas to Phoenix ($2.40) compared to shipping from
Santa Fe to Salt Lake City ($4.70) and from Santa Fe to Phoenix ($3.40), the company would
benefit from dropping these restrictions and utilizing the more cost-effective distribution
routes.
Solution 3
Allowing direct shipments from El Paso to San Antonio, and from San Bernardino to LA and San
Diego add three new arcs to the network model. We add
XA5,
XB11, &
XB12
to the objective function. Additionally, we adjust the demand constraints for San Antonio, LA,
and San Diego to account for the direct shipments from the production plants. The results are
shown below in Figure 5.
Figure 5. Optimal solution with direct-to-customer
shipments
The value of
XA5 = 4,880 indicates
that 4,880 units are being shipped directly from El Paso to San Antonio. Similarly,
XB11 = 8,580 indicates
that 8,580 units are shipped directly from San Bernardino to LA, while
XB12 = 4,460 shows
that 4,460 units are shipped directly from San Bernardino to San Diego. This solution report
highlights a $248,876 reduction in the total cost by implementing these direct-to-customer
shipping routes, translating to a 40% savings compared to the previous supply chain model. Based
on this analysis, it is recommended that Darby Company adopts direct-to-customer shipping from
its production plants and removes the existing limitations on shipping from distribution
centers.